Kendi kayıtlarınızı güncelliyorsanız türünün yalnızca dokuzuncusu veya D(9) 286 386 577 668 298 411 128 469 151 667 598 498 812 366’ya eşit olarak hesaplanır. Bu 42 haneli canavar, 1991’de keşfedilen 23 haneli D(8)’i takip ediyor.

Matematikçi olmayanlar için, bırakın üzerinde çalışmayı, Dedekind sayısı kavramını kavramak bile zordur. Aslında hesaplamalar o kadar karmaşık ve o kadar büyük sayılar içeriyor ki, D(9)’un keşfedilip keşfedilmeyeceği kesin değildi.

–   Almanya’daki Paderborn Üniversitesi’nden bilgisayar bilimcisi Lennart Van Hirtum:

“32 yıl boyunca D(9)’un hesaplanması açık bir zorluktu ve bu sayıyı hesaplamanın mümkün olup olmayacağı şüpheliydi”

Dedekind sayısının merkezinde Boolean işlevleri veya doğru ve yanlış ya da 0 ve 1 gibi yalnızca iki durumdan oluşan girişlerden bir çıktı seçen bir tür mantık bulunur…

Monoton Boolean işlevleri, bir girişte 0’ın 1 ile değiştirilmesinin çıkışın 1’den 0’a değil, yalnızca 0’dan 1’e değişmesine neden olacak şekilde mantığı kısıtlayan işlevlerdir.

Araştırmacılar bunu 1’ler ve 0’lar yerine kırmızı ve beyaz renkleri kullanarak tanımlıyor ancak fikir aynı.

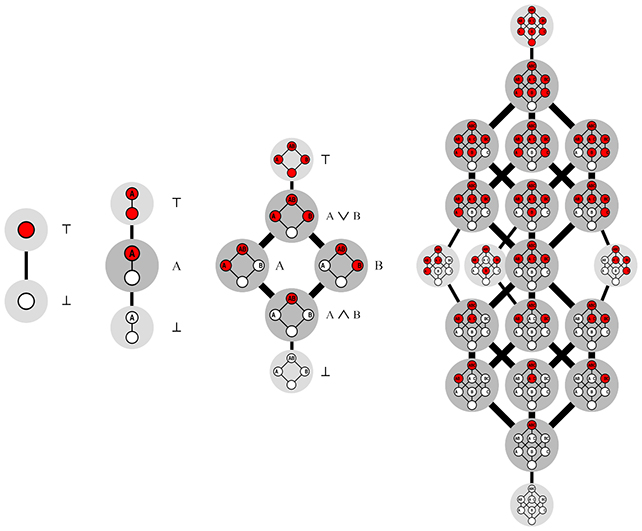0, 1, 2 ve 3 boyutları için Dedekind sayılarını oluşturan kesimlerin gösterimi. (Paderborn Üniversitesi)

–  Van Hirtum:

“Temel olarak, iki, üç ve sonsuz boyutlardaki monoton bir Boole fonksiyonunu, n boyutlu bir küple oynanan bir oyun gibi düşünebilirsiniz..

Küpü bir köşede dengede tutuyorsunuz ve ardından geri kalan köşelerin her birini beyaz veya kırmızıya renklendiriyorsunuz..

İlk birkaçı oldukça basittir. Matematikçiler D(1)’i sadece 2, sonra 3, 6, 20, 168 olarak sayarlar…

1991 yılında Cray-2 süper bilgisayarının (o zamanın en güçlü süper bilgisayarlarından biri) ve matematikçi Doug Wiedemann’ın D(8)’i hesaplaması 200 saat sürdü.

D(9) sonunda D(8)’in neredeyse iki katı uzunluğa ulaştı ve özel bir tür süper bilgisayar gerektiriyordu: birden fazla hesaplamayı paralel olarak gerçekleştirebilen, Alan Programlanabilir Kapı Dizileri (FPGA’ler) adı verilen özel birimleri kullanan bir bilgisayar. Bu, ekibi Paderborn Üniversitesi’ndeki Noctua 2 süper bilgisayarına yönlendirdi.

Paderborn Paralel Hesaplama Merkezi’nin (PC2) başkanı bilgisayar bilimcisi Christian Plessl, “FPGA’lerle zorlu kombinatoryal problemleri çözmek umut verici bir uygulama alanıdır ve Noctua 2, deneyin gerçekleştirilebileceği dünya çapındaki birkaç süper bilgisayardan biridir” diyor . ) Noctua 2’nin tutulduğu yer..

Noctua 2’ye çalışacak bir şey kazandırmak için daha fazla optimizasyon yapılması gerekiyordu. Süreci daha verimli hale getirmek için formüldeki simetrileri kullanan araştırmacılar, süper bilgisayara, 5,5*10^18 terim içeren büyük bir toplam verdi (Dünyadaki kum tanelerinin sayısı 7,5*10^ olarak tahmin ediliyor). 18, karşılaştırma için).

Beş ay sonra Noctua 2 bir cevap buldu ve artık D(9) elimizde. Araştırmacılar şimdilik D(10)’a herhangi bir atıfta bulunmadı ancak onu bulmanın 32 yıl daha sürebileceğini tahmin edebiliyoruz.

Makale Eylül ayında Norveç’teki Uluslararası Boole Fonksiyonları ve Uygulamaları Çalıştayında (BFA) sunuldu .